INSTITUCIÓN EDUCATIVA NUESTRA SEÑORA DEL PILAR

ALDANA - NARIÑO

TOMADO DE: http://www.calculo.cc/temas/temas_bachillerato/primero_ciencias_sociales/funciones_elementales/teoria/coseno.html

Función coseno

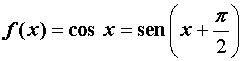
Su gráfica será idéntica a la del seno pero con un desfase de π/2 , es decir, se produce una traslación de π/2 a la izquierda.

Las características fundamentales de la función coseno son las siguientes:

1) Su dominio es R y es continua.

2) Su recorrido es [- 1, 1] ya que - 1 ≤ cos x ≤ 1 .

3) Corta al eje X en los puntos π/2 + k·π con k∈Z .

Corta al eje Y en el punto (0, 1) .

4) Es par, es decir, simétrica respecto al eye Y.

cos (x) = cos (- x)

5) Es estrictamente creciente en los intervalos de la forma (a, b) donde a = - π + 2·k·π y b = 0 + 2·k·π siendo k∈Z .

Es estrictamente decreciente en los intervalos de la forma (a, b) donde a = 0 + 2·k·π y b = π + 2·k·π siendo k∈Z .

6) Tiene infinitos máximos relativos en los puntos de la forma (2·k·π, 1) con k∈Z .

Tiene infinitos mínimos relativos en los puntos de la forma (π + 2·k·π, - 1) con k∈Z .

7) Es periódica de periodo 2π .

cos (x) = cos (x + 2π)

La función f(x) = cos (k·x) es periódica de periodo p = 2π/k

Para |k|>1 el periodo disminuye y para 0< |k| <1 el periodo aumenta.

8) Está acotada superiormente por 1 e inferiormente por - 1.

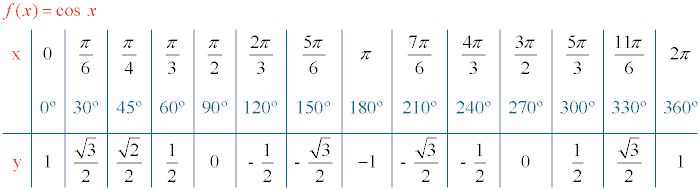
Amplitud, periodo y traslación

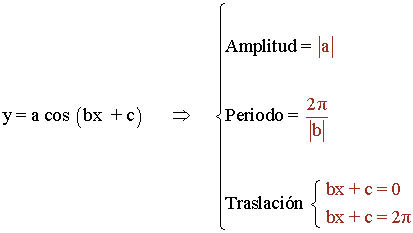
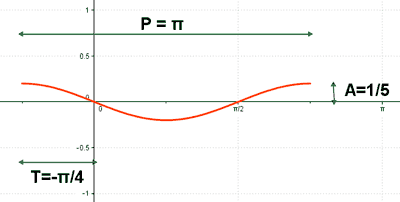
Amplitud = |1/5| = 1/5

Periodo = 2π/|2| = 2π/2 = π

Traslación : 2x + π/2 = 0 ⇒ x = - π/4
2x + π/2 = 2π ⇒ x = 3π/4